Cubic Splines

Unlike previous methods of Interpolating,

Spline interpolation does not produce the same unique interpolating polynomial, as with the Lagrange method, Vandermonde matrix method, or Newton’s divided difference method.  Spline interpolation addresses some of the error concerns of polynomial interpolation: low-degree polynomial interpolation can give poor approximations, while high-degree interpolating polynomials may introduce large over-correcting oscillations.  Spline interpolation uses multiple lower-degree polynomials, such that high-order error is reduced.  Because each spline is also using fewer terms, problems arising from using a large number of data points, such as vanishing determinants in Vandermonde matrices, can be avoided.  Cubic splines create a series of piecewise cubic polynomials.

For n+1 data points:

(x_0,y_0),(x_1,y_1),...,(x_n,y_n)

The interpolating splines are as follows:

S(x) = \left\{\begin{matrix} S_0(x) & x \in [x_0, x_1] \\ S_1(x) & x \in [x_1, x_2] \\ \vdots & \vdots \\ S_{n-1}(x) & x \in [x_{n-1}, x_n] \end{matrix}\right.

Where S_i(x) = a_i + b_i(x-x_i) + c_i(x-x_i)^2 + d_i(x-x_i)^3

Which is simplified by using the substitution h_i = (x-x_i) , giving:

S_i(x) = a_i + b_ih_i + c_ih_i^2 + d_ih_i^3

To guarantee the smooth continuity of the interpolating Spline S(x) , we have the following conditions:

1) S_i(x_i) = y_i So that the splines properly interpolate the given points.

2) S_{i-1}(x_i) = S_i(x_i) so that two adjacent splines’ endpoints are equal.

3) S'_{i-1}(x_i) = S'_i(x_i) so that two adjacent splines’ first derivatives at endpoints are equal.

4) S''_{i-1}(x_i) = S''_i(x_i) so that two adjacent splines’ second derivatives at endpoints are equal.

As stated on the Wikipedia page, the first requirement imposes n+1 restrictions, while requirements 2,3,4 impose n-1 restrictions each, for a total n+1 + 3(n-1) = 4n-2.  Because we are finding 4 coefficients for each of n polynomials, we need 4n restrictions.  Clamped splines use fixed bounding conditions for S(x) at x_0 \text{ and } x_n, while natural splines use a fixed second derivative, such that S''(x_0) = S''(x_n) = 0.  Our analysis will use natural splines.

We will use these 4 rules and 2 bound conditions to construct a tri-diagonal matrix which can be efficiently solved, giving the coefficients of each spline.

Ensuring Rule 2:

First, the simple form of S_{i-1}(x) :

S_{i-1}(x) = a_{i-1} + b_{i-1}h_{i-1} + c_{i-1}h_{i-1}^2 + d_{i-1}h_{i-1}^3

Rules 1 and 2 together give us: y_i = S_{i}(x_i) = S_{i-1}(x_i)

Combining these two equations gives us:

y_i = S_{i-1}(x_i) = a_{i-1} + b_{i-1}h_{i-1} + c_{i-1}h_{i-1}^2 + d_{i-1}h_{i-1}^3

Since a_{i-1} = y_{i-1} :

y_i = y_{i-1} + b_{i-1}h_{i-1} + c_{i-1}h_{i-1}^2 + d_{i-1}h_{i-1}^3

Where h_{i-1} = (x_i-x_{i-1})

Ensuring Rule 3:

Next, we ensure first derivatives match:

S'_{i-1}(x_i) = S'_i(x_i)

Taking the derivative of the simple form of a spline, we have:

S'_i(x) = b_i + 2c_ih_i + 3d_ih_i^2

We combine S'_i(x_i) = b_i , with the two previous equations, much as we did in step 1:

b_i = S'_i(x_i) = S'_{i-1}(x_i) = b_{i-1} + 2c_{i-1}h_{i-1} + 3d_{i-1}h_{i-1}^2

b_i = b_{i-1} + 2c_{i-1}h_{i-1} + 3d_{i-1}h_{i-1}^2

Ensuring Rule 4:

We repeat step 2, but for the second derivative, using:

S''_i(x) = 2c_i + 6d_ih_i and S''_i(x_i) = 2c_i

We are ensuring rule 4: S''_{i-1}(x_i) = S''_i(x_i)

Combining these, we have:

2c_i = S''_i(x_i) = S''_{i-1}(x_i) = 2c_{i-1} + 6d_{i-1}h_{i-1}

Giving:

2c_i = 2c_{i-1} + 6d_{i-1}h_{i-1}

Solving for 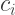c_i :

With our bound conditions S''(x_0) = S''(x_n) = 0 , we can now solve for c_i .  What follows is an algebraic manipulation to remove b and d from the equation so that c is in terms of h, y.

\Big(Eq 1\Big) y_i = y_{i-1} + b_{i-1}h_{i-1} + c_{i-1}h_{i-1}^2 + d_{i-1}h_{i-1}^3

\Big(Eq 2\Big) b_i = b_{i-1} + 2c_{i-1}h_{i-1} + 3d_{i-1}h_{i-1}^2

\Big(Eq 3\Big) 2c_i = 2c_{i-1} + 6d_{i-1}h_{i-1}

First we solve Eq.1 for b_{i-1} and then increment all indices and solve for b_i.  In both cases, we divide by h_{i-1} or h_{i} respectively:

\Big(Eq 4\Big) b_{i-1} = \frac{y_i-y_{i-1}}{h_{i-1}} - c_{i-1}h_{i-1} - d_{i-1}h_{i-1}^2

\Big(Eq 5\Big) b_{i} = \frac{y_{i+1}-y_{i}}{h_{i}} - c_{i}h_{i} - d_{i}h_{i}^2

Next, we rearrange Eq.3:

2c_i-2c_{i-1} = 6d_{i-1}h_{i-1}

Multiply both sides by h_{i-1} and divide both sides by 2 to give:

\Big(Eq 6\Big) h_{i-1}(c_i-c_{i-1}) = 3d_{i-1}h_{i-1}^2

Next, solve Eq.2 for the d term as follows:

\Big(Eq 7\Big) 3d_{i-1}h_{i-1}^2 = b_i - b_{i-1} - 2c_{i-1}h_{i-1}

Substitute this into the right-hand side of Eq.6 to get:

h_{i-1}(c_i-c_{i-1}) = b_i - b_{i-1} - 2c_{i-1}h_{i-1}

Move the c term from the right side to the left:

2c_{i-1}h_{i-1} + h_{i-1}(c_i-c_{i-1}) = (b_i-b_{i-1})

Combine like terms on the left side to get:

\Big(Eq 8\Big) h_{i-1}(c_i+c_{i-1}) = (b_i-b_{i-1})

By substituting Eq.4 (for b_{i-1}) and Eq.5 (for b_{i}) into Eq.8 we get:

\begin{array}{l} h_{i-1}(c_i+c_{i-1}) = (\frac{y_{i+1}-y_{i}}{h_{i}} - c_{i}h_{i} - d_{i}h_{i}^2) - (\frac{y_i-y_{i-1}}{h_{i-1}} - c_{i-1}h_{i-1} - d_{i-1}h_{i-1}^2) \end{array}

Moving both c terms to the left gives:

\begin{array}{l} c_{i}h_{i} - c_{i-1}h_{i-1} + h_{i-1}(c_i+c_{i-1}) = (\frac{y_{i+1}-y_{i}}{h_{i}} - d_{i}h_{i}^2) - (\frac{y_i-y_{i-1}}{h_{i-1}} - d_{i-1}h_{i-1}^2) \end{array}

The c_{i-1}h_{i-1} terms cancel on the left and we rearrange the right side to get:

\begin{array}{l} \Big(Eq 9\Big) c_{i}h_{i} + c_ih_{i-1} = (\frac{y_{i+1}-y_{i}}{h_{i}} -\frac{y_i-y_{i-1}}{h_{i-1}}) + (d_{i-1}h_{i-1}^2 - d_{i}h_{i}^2) \end{array}

Now we solve Eq.6 for d_{i-1}h_{i-1}^2 :

\Big(Eq 10\Big) d_{i-1}h_{i-1}^2 = \frac{1}{3}h_{i-1}(c_i-c_{i-1})

And for d_{i}h_{i}^2 :

\Big(Eq 11\Big) d_{i}h_{i}^2 = \frac{1}{3}h_{i}(c_{i+1}-c_{i})

We can substitute Eq.10 and Eq.11 into Eq.9 and factor the \frac{1}{3}, finally removing the d_i terms:

\begin{array}{l} c_{i}h_{i} + c_ih_{i-1} = (\frac{y_{i+1}-y_{i}}{h_{i}} -\frac{y_i-y_{i-1}}{h_{i-1}}) + \frac{1}{3}\Big(h_{i-1}(c_i-c_{i-1}) - h_{i}(c_{i+1}-c_{i})\Big) \end{array}

Multiplying by 3 to remove fractions and moving the c_i terms on the right to the left:

\begin{array}{l} 3c_{i}h_{i} + 3c_ih_{i-1} - \Big(h_{i-1}(c_i-c_{i-1}) - h_{i}(c_{i+1}-c_{i})\Big) = 3\Big(\frac{y_{i+1}-y_{i}}{h_{i}} -\frac{y_i-y_{i-1}}{h_{i-1}}\Big) \end{array}

Combining like terms on the left:

\begin{array}{l} c_{i-1}h_{i-1} + 2c_ih_{i-1} + 2c_ih_i + c_{i+1}h_i = 3\Big(\frac{y_{i+1}-y_{i}}{h_{i}} -\frac{y_i-y_{i-1}}{h_{i-1}}\Big) \end{array}

And finally expressing the left as a combination of c:

\begin{array}{l} \Big(Eq 12\Big) c_{i-1}h_{i-1} + 2c_i(h_{i-1} + h_i) + c_{i+1}h_i = 3\Big(\frac{y_{i+1}-y_{i}}{h_{i}} -\frac{y_i-y_{i-1}}{h_{i-1}}\Big) \end{array}

We can now express this as a tri-diagonal matrix times c and using an efficient recursive method to solve the tri-diagonal, get the values of c:

\begin{array}{l} \begin{bmatrix} 2(h_0+h_1) & h_1 & \text{} & \text{} & \text{} \\ h_1 & 2(h_1+h_2) & h_2 & \text{} & \text{} \\ \text{} & \ddots & \ddots & \ddots & \text{} \\ \text{} & \text{} & h_{n-3} & 2(h_{n-3}+h_{n-2}) & h_{n-2} \\ \text{} & \text{} & \text{} & 2(h_{n-2}+h_{n-1}) & h_{n-1} \\ \end{bmatrix} \begin{bmatrix} c_1 \\ c_2 \\ \vdots \\ c_{n-2} \\ c_{n-1} \\ \end{bmatrix} = 3\begin{bmatrix} \frac{y_{2}-y_{1}}{h_{1}} -\frac{y_1-y_{0}}{h_{0}} \\ \vdots \\ \vdots \\ \vdots \\ \frac{y_{n}-y_{n-1}}{h_{n-1}} -\frac{y_{n-1}-y_{n-2}}{h_{n-2}} \\ \end{bmatrix} \end{array}

Solving the remaining coefficients:

With c known, we can easily calculate the remaining coefficients:

We solve Eq.3 for d_{i-1} and then increment indices:

d_{i-1} = \frac{1}{3}\frac{c_i - c_{i-1}}{h_{i-1}}

d_{i} = \frac{1}{3}\frac{c_{i+1} - c_{i}}{h_{i}}

We know that a_i = y_i to satisfy S_i(x_i) = y_i

Finally, we can calculate b_i using Eq.5:

\Big(Eq 5\Big) b_{i} = \frac{y_{i+1}-y_{i}}{h_{i}} - c_{i}h_{i} - d_{i}h_{i}^2

Code + Example:

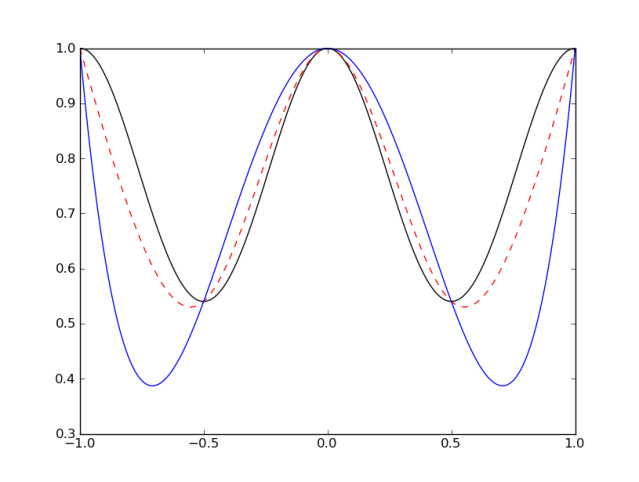
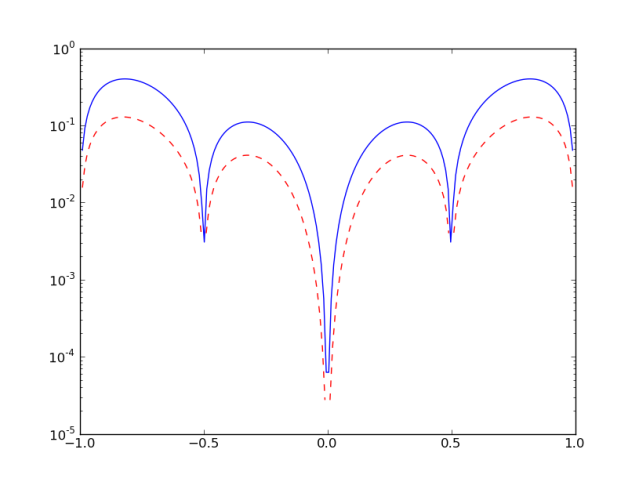
This python code has a function Spline(data) that takes a set of ordered x,y pairs and returns a list of tuples, where each tuple represents the values (a_i,b_i,c_i,d_i,x_i .  The function splinesToPlot(splines,xn,res) takes a set of spline coefficient tuples, a right endpoint, and a grid resolution and creates X and Y vectors corresponding to the plot of the spline set.  The two pictures below were generated using this python code to compare the Lagrange interpolating polynomial and Spline Interpolation using 5 data points.  The function being estimated is the same as in previous sections: cos(sin(\pi x)) .  The second picture is an absolute error log plot of each method.

In both images, the red dashed line represents the Cubic Spline interpolation, while the solid blue line is the Lagrange interpolating polynomial.  In the first image, the black line is the actual function.

Leave a comment